|
|
|
|
QUELS SONT LES EFFETS DE L'OBSTRUCTION ?
Les images réelles et de synthèse, les courbes, les dessins et les textes sont propriété de l'auteur et ne peuvent être reproduits ou utilisés sans autorisation
Qu'est-ce que l'obstruction ?
L'obstruction d'un télescope est représentée par son miroir secondaire (et son support) qui stoppe la partie centrale du faisceau lumineux.
La quantité d'obstruction varie selon l'instrument considéré. Elle dépend du principe optique du télescope (Newton, Schmidt-Cassegrain, etc.) et de certains choix de réalisation liés notamment au champ de pleine lumière (c'est-à-dire sans vignetage) recherché. La valeur de l'obstruction varie habituellement, en pourcentage du diamètre de l'instrument, de 15 % à 35 %. Certains instruments dédiés à la photographie à grand champ du ciel profond peuvent présenter une obstruction supérieure à 40 %.
Dans le but de présenter des chiffres plus flatteurs en apparence, certains constructeurs expriment l'obstruction de leurs télescopes non pas en fraction du diamètre mais en fraction de la surface collectrice de l'instrument. L'obstruction en surface se déduit de l'obstruction en diamètre en élevant celle-ci au carré. Exemple : une obstruction de 20 % en diamètre (soit 40 mm sur un 200 mm) correspond à une obstruction de 0,04 (0,20 au carré) soit 4 % en surface. Inversement, un télescope obstrué à 10 % en surface correspond à 32 % (racine carrée de 0,1) d'obstruction en diamètre. D'autres constructeurs indiquent le diamètre du miroir secondaire et non de son support, ce qui permet également d'améliorer artificiellement les chiffres, alors que c'est évidemment le diamètre du support qui compte.
Les effets de l'obstruction sont de deux ordres : la quantité de lumière captée par l'instrument est diminuée, et le contraste de l'image fournie par l'instrument est modifié.
La diminution de lumière recueillie par le télescope est directement exprimée par la valeur de son obstruction en surface. Un télescope obstrué à 20 % perd ainsi 4 % de lumière, tandis qu'un télescope obstrué à 33 % perd 11 % de lumière. On constate que, même dans les fortes obstructions, la perte de lumière est peu importante : une ouverture de 250 mm obstruée à 34 % recueille la même quantité de lumière qu'une ouverture non obstruée de 235 mm de diamètre.
Quels sont les effets de l'obstruction sur la figure d'Airy ?
La présence d'une obstruction modifie la figure de diffraction (figure d'Airy) d'une étoile délivrée par l'instrument. Cette figure, visible à fort grossissement, se compose d'un disque central (faux disque) entouré d'anneaux de luminosité décroissante (figures ci-dessous). L'obstruction a pour effet de diminuer la lumière contribuant au disque central (dont le diamètre est légèrement diminué), au profit des anneaux qui sont renforcés. Les figures ci-dessous présentent l'apparence visuelle de la figure d'Airy pour des télescopes obstrués à 0 %, 20 % et 33 %.
|
|
|
|
Même si le changement d'apparence de la figure d'Airy semble considérable (les images ci-dessus sont affichées en échelle logarithmique pour correspondre à la vision humaine), l'effet joue sur des niveaux d'intensité faibles, comme le montrent les profils ci-dessous : entre 0 % et 33 % d'obstruction, l'intensité maximale du premier anneau de diffraction passe de 1,7 % à 5,4 % de l'intensité maximale du disque. Il est faux d'affirmer qu'en présence d'obstruction, le disque central fusionne avec le premier anneau de diffraction.
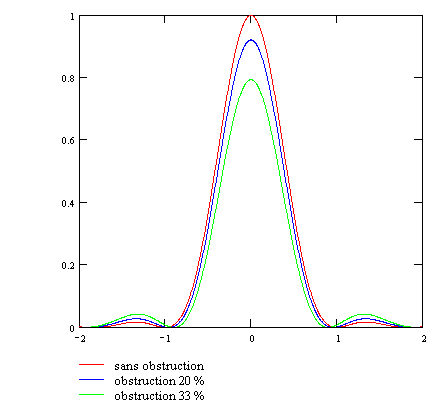
Quels sont les effets de l'obstruction sur le contraste ?
La courbe de contraste de l'instrument (cf. Qu'est-ce qu'une courbe de FTM ?) est modifiée par l'obstruction d'une manière complexe, ainsi que le montre la figure ci-dessous. En présence d'obstruction, le contraste diminue effectivement par rapport au même instrument non obstrué, mais uniquement dans les basses et moyennes fréquences spatiales (partie gauche de la courbe). A l'inverse, dans les hautes fréquences spatiales (partie droite), le contraste n'est pas diminué, il est même très légèrement accru.
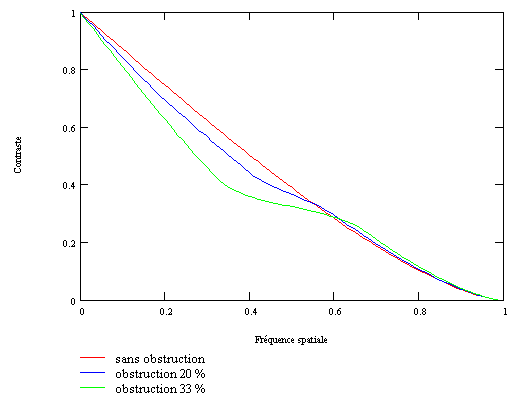
La figure ci-dessous présente les courbes relatives à des instruments obstrués respectivement à 20 % et à 33 %. Le prolongement de la partie gauche de chaque courbe indique à quel instrument non obstrué il équivaut en contraste dans les basses fréquences. Il apparaît qu'un instrument obstrué à 33 % équivaut dans les basses fréquences à un instrument non obstrué d'un diamètre 33 % inférieur (170 mm pour 250 mm). Un télescope obstrué à 20 % équivaut quant à lui à un instrument non obstrué d'un diamètre environ 15 % inférieur (210 mm pour 250 mm).
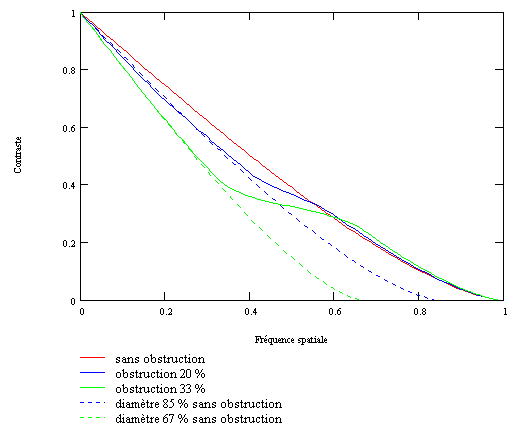
Une règle empirique déduite de ces résultats est qu'un instrument obstrué de diamètre D et d'obstruction d, dans les basses fréquences, équivaut à un instrument non obstrué d'un diamètre effectif Deff valant :
Deff = D - d
(cette règle est un peu pessimiste pour les faibles obstructions).
L'examen des effets sur le pouvoir de résolution de l'instrument conduit à séparer deux cas :
1) les structures de contraste élevé : Lune, étoile double, division de Cassini, ombre de satellite ou d'anneau, bord de planète. La limite de résolution se situant près de l'extrémité droite de la courbe (cf. Qu'est-ce que la haute résolution ?), elle n'est pas modifiée par l'obstruction.
2) les structures de contraste faible : surfaces de Mars, Jupiter et Saturne. La limite de résolution se situe à une fréquence plus basse que dans le cas précédent. Pour des détails de très faible contraste, cette limite peut être placée avant le point d'intersection des courbes. Dans ce cas, elle est inférieure pour l'instrument obstrué. Comme pour le contraste dans les basses fréquences, la résolution de l'instrument est alors équivalente à celle d'un instrument non obstrué de diamètre Deff.
Le fait que la limite de résolution se situe à droite ou à gauche de l'intersection des courbes (et donc qu'il y ait ou pas perte de résolution) dépend du contraste intrinsèque de l'objet (qui peut varier selon la longueur d'onde : Jupiter est plus contrasté dans le bleu que dans le rouge). Il dépend également de la technique employée : CCD, photographie ou visuel (le seuil de contraste est différent : 2 % environ pour l'observation visuelle dans des conditions de luminosité suffisantes, probablement 0,5 % en CCD). Aucune règle générale ne peut donc être donnée concernant la perte de résolution sur les surfaces peu contrastées. Néanmoins, la résolution effective est au minimum celle d'un instrument non obstrué de diamètre Deff.
Ces résultats sont valables uniquement si l'instrument est optiquement bon et bien réglé. Dans le cas contraire, la courbe de FTM est écrasée, la limite de résolution est diminuée et la perte de résolution affecte tous les objets, y compris les objets contrastés tels que la Lune. Mais dans cette situation peut-on encore parler de haute résolution ?
Une araignée, bien qu'elle provoque des aigrettes sur les étoiles brillantes, n'a aucune influence perceptible sur le contraste et la résolution des images lunaires et planétaires. Pour la haute résolution, il n'est donc pas nécessaire d'employer des astuces telles que des lames courbes.
Quels sont les effets de l'obstruction sur des images planétaires et lunaires ?
Les images lunaire et planétaires ci-dessous (colonne de gauche) présentent ce que pourrait montrer un instrument de 150 mm non obstrué. Les colonnes suivantes contiennent des simulations d'obstructions respectives de 20 % et 33 % sur le même instrument.
|
Sans obstruction |
Obstruction 20 % |
Obstruction 33 % |
|
|
|
|
|
|
|
|
La modification des performances due à l'obstruction de 20 % est peu sensible. Une telle obstruction peut être considérée comme presque négligeable, elle est probablement difficile à distinguer en pratique d'une obstruction nulle. L'obstruction de 33 % a des effets plus nets sur le contraste des images : l'objet apparaît globalement moins contrasté. Cependant, il est net que sur les craterlets et rainures lunaires, le pouvoir de résolution de l'instrument n'est pas modifié. A l'inverse, sur les détails très peu contrastés (bandes nuageuses de Jupiter et Saturne), on peut noter une baisse de résolution.
Conclusion
Les effets de l'obstruction sont les suivants :
|
1) le contraste global des images est diminué, l'instrument (diamètre D, obstruction d) ayant approximativement le même rendement qu'un instrument non obstrué de diamètre Deff = D - d 2) le pouvoir de résolution de l'instrument n'est pas modifié sur les objets et détails contrastés : 3) le pouvoir de résolution peut être diminué sur les objets peu contrastés : surfaces de Mars, Jupiter et Saturne. La résolution effective dépend du contraste de l'objet et de la technique employée, elle est au minimum celle d'un instrument non obstrué de diamètre Deff |
Du strict point de vue de l'obstruction, on obtient les équivalences suivantes :
|
Diamètre télescope |
Diamètre lunette équivalent |
Diamètre lunette équivalent |
Diamètre lunette équivalent |
Diamètre lunette équivalent |
|
300 mm |
200 mm |
200 à 300 mm (1) |
300 mm |
280 mm |
|
250 mm |
170 mm |
170 à 250 mm (1) |
250 mm |
235 mm |
|
225 mm |
150 mm |
150 à 225 mm (1) |
225 mm |
210 mm |
|
200 mm |
130 mm |
130 à 200 mm (1) |
200 mm |
190 mm |
|
150 mm |
100 mm |
100 à 150 mm (1) |
150 mm |
140 mm |
(1) : selon le contraste de l'objet et la technique employée
(2) : en supposant identiques les coefficients de transmission des optiques
L'obstruction, bien qu'ayant des effets qui peuvent être non négligeables sur le contraste et la résolution des images planétaires, n'est absolument pas rédhibitoire pour la haute résolution. Il ne faut pas perdre de vue que, sur les planètes, l'obstruction ne peut à elle seule rendre un télescope de 250 mm inférieur à une lunette de 170 mm. Sur la Lune, le télescope bénéficie de son plein pouvoir de résolution. Ce n'est pas un hasard si, comme l'a montré Jean Dragesco dans High Resolution Astrophotography (cf. Bibliographie), les meilleures images planétaires et lunaires à haute résolution réalisées ces dernières années ont toutes été prises avec des télescopes de 200 à 400 mm de diamètre dont certains étaient obstrués à plus de 30 %.
Bien sûr, toutes choses étant égales par ailleurs, mieux vaut un instrument faiblement obstrué qu'un instrument fortement obstrué. Mais il serait absurde de se focaliser sur l'obstruction au détriment de toute autre considération et d'imaginer qu'un instrument peu obstrué est obligatoirement meilleur qu'un autre plus obstrué. Car en matière de dégradation d'image, l'obstruction est l'arbre qui cache la forêt. La production photographique et CCD planétaire amateur nous montre que la quasi-totalité des instruments en service n'est pas limitée par l'obstruction mais par d'autres causes de dégradation telles qu'une décollimation, une mise en température défectueuse ou une mauvaise focalisation, souvent à un point tel que l'obstruction devient un phénomène négligeable. Les qualités et les défauts d'un instrument ne se limitent pas à son obstruction, il y a d'autres critères plus importants en pratique : facilité de mise en température, stabilité d'image, fiabilité et précision du système de focalisation, fiabilité du système de maintien des optiques, etc. Il ne suffit pas d'avoir une optique déclarée bonne au test de Foucault et faiblement obstruée pour obtenir automatiquement de bons résultats sur le terrain.
Pourtant, on entend parfois des affirmations catégoriques telles que : " l'obstruction diminue fortement le pouvoir de résolution ", " un instrument obstrué perd 50 % de ses capacités " " un instrument obstrué à 30 % est inutilisable en haute résolution ", ou "l'obstruction a moins d'effets en CCD qu'en visuel". Affirmations très excessives car contredites par les lois de la diffraction et par des expériences menées avec un minimum de rigueur. Lorsque ces opinions sont issues d'une comparaison entre instruments sur le terrain, elles relatent certes une expérience réellement vécue mais elles expriment les effets d'autres facteurs que l'obstruction : principes optiques différents, sensibilité à la turbulence différente, diamètres différents, qualités optiques différentes, grossissements différents, réglages différents, etc. En particulier, la plupart des télescopes en service souffre de décollimation (même si leurs propriétaires pensent le contraire), ce qui provoque un effondrement des performances bien supérieur aux dommages causés par l'obstruction (cf. La collimation). Le seul moyen valable d'observer les effets réels de l'obstruction est d'utiliser un unique instrument (lunette ou Newton faiblement obstrué) que l'on obstrue artificiellement à l'aide de disques en métal de diamètres variés, afin de supprimer toutes les autres différences qui sont généralement prépondérantes.
Pour un amateur qui construit son instrument, il peut même être risqué de chercher à minimiser à tout prix la taille du miroir secondaire. Si celui-ci est sous-dimensionné, la périphérie du faisceau lumineux est perdue, ce qui conduit à une perte de lumière et à une augmentation de l'obstruction effective (l'inverse du but recherché !). Surtout, de nombreux miroirs, qu'ils soient de fabrication industrielle ou artisanale, présentent des défauts de forme sur leur périphérie (bord rabattu ou relevé). Dans ce cas, vouloir exploiter coûte que coûte l'extrême bord du miroir secondaire peut provoquer une dégradation des performances de l'instrument bien plus importante que ce qu'aurait provoqué un petit supplément d'obstruction "de sécurité". Le mieux est parfois l'ennemi du bien...